I didn't think anything about your code. I just tried giving it lots of random inputs, to measure the error in my approximation, and this revealed some problems in your results. I am just pointing them out.

Try to give this input to your function:

q0 = (0.584283 0.670586 0.41005 0.201958), q1 = (-0.651197 -0.648167 -0.342918 -0.195523), t=0.668532

Initially, a=0.331468, b=0.668532. Then you compute d=-0.995236, c=3.04394 (if you use d instead of fabsf(d)), then  b=10.257, a=8.68029, b=9.17167, b=-9.17167, which makes the answer be (11.0443 11.7657 6.70448 3.54633), which is obviously not a length-1 vector.
 

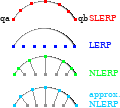
My "first-order correction to LERP" was meant to modify the straight line in LERP to get closer to the arc along the unit sphere. I don't know if the approximation is good enough to be visually acceptable in a game.

Here's a much better approximation, which still only uses multiplication and addition, so it should be very fast.

float approx_a(float d, float t) {
  float const x1 = 0.555713f;
  float const x2 = 0.281959f;
  float const x3 = -0.207537f;
  float const x4 = 0.143091f;
  float const x5 = -0.0925688f;
  return (1.0f - t) * (1.0 + (1.0f - d * x1 - t * x2 - d*d*x3 - t*t*x4 - d*t*x5) * t * (1.0 - d));
}

void approximate_slerp(float const qa[4], float const qb[4], float t, float ret[4]) {
  float d = qa[0] * qb[0] + qa[1] * qb[1] + qa[2] * qb[2] + qa[3] * qb[3];

  float a = approx_a(std::abs(d), t);
  float b = copysign(approx_a(std::abs(d), 1.0f - t), d);

  ret[0] = qa[0] * a + qb[0] * b;
  ret[1] = qa[1] * a + qb[1] * b;
  ret[2] = qa[2] * a + qb[2] * b;
  ret[3] = qa[3] * a + qb[3] * b;

  // The quaternion computed above might be good enough. Its main flaw might be that it doesn't have length exactly 1.
  // If this is important, you can use the lines below, which will make the length much closer to 1.
  
  float l2_norm = ret[0]*ret[0] + ret[1]*ret[1] + ret[2]*ret[2] + ret[3]*ret[3];
  float inv_length = 1.5 - 0.5 * l2_norm;
  ret[0] *= inv_length;
  ret[1] *= inv_length;
  ret[2] *= inv_length;
  ret[3] *= inv_length;
}

Rearranging things a bit to make the compiler's life easier, you can get this:

void approximate_slerp2(float const qa[4], float const qb[4], float t, float ret[4]) {
  float const x1 = 0.555713f;
  float const x2 = 0.281959f;
  float const x3 = -0.207537f;
  float const x4 = 0.143091f;
  float const x5 = -0.0925688f;

  float d = qa[0] * qb[0] + qa[1] * qb[1] + qa[2] * qb[2] + qa[3] * qb[3];
  float ad = std::abs(d);

  // T<n> are quantities that only depend on t, so they can be calculated once for many bones
  float T1 = t * (1.0f - t);
  float T2 = 1.0f - t * (x2 + t*x4);
  float T3 = 1.0f - (1.0f-t) * (x2 +(1.0f-t)*x4);

  // C<n> are quantities that are shared in the computation of a and b. I'm not sure if the compiler needs help here, but it shouldn't hurt to organize things like this.
  float C1 = T1 * (1.0f - ad);
  float C2 = ad * (x1 + ad * x3);
  float C3 = ad * x5;

  float a = 1.0f - t + C1 * (T2 - C2 - t * C3);
  float b = copysign(t + C1 * (T3 - C2 - (1.0f-t) * C3), d);

  ret[0] = qa[0] * a + qb[0] * b;
  ret[1] = qa[1] * a + qb[1] * b;
  ret[2] = qa[2] * a + qb[2] * b;
  ret[3] = qa[3] * a + qb[3] * b;

  float final_l2 = ret[0]*ret[0] + ret[1]*ret[1] + ret[2]*ret[2] + ret[3]*ret[3];
  float inv_length = 1.5 - 0.5*final_l2;

  ret[0] *= inv_length;
  ret[1] *= inv_length;
  ret[2] *= inv_length;
  ret[3] *= inv_length;
}

Hi,

Oh I see what you mean, in that case thank you very much for the input and test quaternions! It is not a unit quaternion for sure! I'll look into it. GLM::mix() only calculates SLERP for positive d (and fallbacks to LERP for all negative values), but I don't like that "workaround".

Thanks for the approximation, but I'm not interested in this kind at all, because as I've said it does not keep constant velocity. Approximating the unit sphere's surface by normalizing the quaternion is just one thing, providing results at equal distances is a totally different issue. Just to be clear, it's the T1,T2,T3 part in your code that causes the trouble for me. I'm all about to speed up SLERP, not to change its characeristics. Just for the sake of the argument, you could approximate SLERP with a _recursive_, reentrant NLERP function, that could keep the velocity, but would also need sqrt to do so, therefore it is questionable if it would be faster at all.

I'm looking for a simple and fast _mm_acos_ps() implementation or a pure sin() or acos() approximation only (which does not modify the balance between t and 1.0-t). You see what I want to achieve is getting results at equal distances, and it doesn't matter if those results are not 100% accurate (as long as their epsilon is much less than the distance between them, no-one would notice). Replacing equal distances with changing ones is noticeable, no matter how accurate each results are.

Thank you very much for your posts, feed back, and efforts! I've fixed that lame and/or bug in the GLSL code.

Thanks,
bzt

Let me explain with a figure.
SLERP provides results between qa and qb on the unit sphere at equal distances (red dots).
LERP provides results between qa and qb on a straight line (blue dots), not on the sphere's surface.
NLERP corrigates this by normalizing the results, so that they are on the unit sphere's surface, however their distances change (see green dots are not at equal distances). This is what I call non-constant velocity.
Finally, your approximated NLERP tries to solve this by calculating results at different distances on the qa-qb straight line, so that after normalization they would be hopefully closer to equal distances (cyan dots). However this isn't guaranteed because of the normalization (in theory may be, but not in practice where limited precision and accumulated error comes in). This kind of approximation can be very useful, no question about that, it is just not what I'm after.

I'm only interested in calculating the red dots in an optimized way, and I don't care if a single result is in an epsilon radius of the perfect red dot position (as long as epsilon is small, incomparable to the distance between two neighbouring red dots).

Hope this clearifies things what I want to achieve, and what I don't.

Cheers
bzt